Converting From Decimal to Base b

Reversing the Conversion Process

In the previous post, we discussed how to convert from base b to decimal (base 10). Besides some basic bookkeeping/organization, the rest of the algorithm was mostly multiplication and addition. For example, we converted the hexadecimal number to base 10:

From a mathematical perspective, you might predict that the steps to reverse this process (converting from base 10 to hexadecimal) will involve a lot of division and subtraction. After all, the inverse operation of multiplication is division and the inverse operation of addition is subtraction. Let’s try it out.

Remember that a hexadecimal (base 16) representation of the decimal (base 10) number will be a sequence of digits, each of which is a coefficient for a power of 16. If we want to find the leftmost digit of the hexadecimal representation of , we need to know the largest integer power, of 16 such that . You can use mental math, guess-and-check, or the integer part of to find out that our desired power of is . Next, perform long division to see how many times goes into :

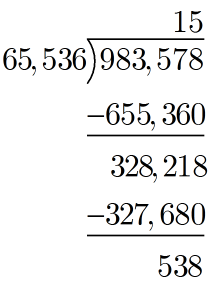
The quotient from this division is , which is a base 10 representation of the first digit of our hexadecimal number. We can easily convert in decimal to in hexadecimal. We now have our first digit of our hexadecimal number! This is a five digit number, , but we still have to fill in these last four squares.

Next, notice that the remainder from our division is . You can think of this as the remaining portion of that has not yet been converted to hexadecimal yet.

We just need to repeat this process on . First, we check if , which it most certainly is not. This means that our next hexadecimal digit after is since there are no that can divide . Now, we’ve gotten our number to .

Next, check if , which it is. So we can repeat our long division step from before:

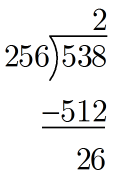
The quotient from this division is , which is our next hexadecimal digit. Our number is almost filled in, . Notice that the remainder from this division step is , which you can think of as the portion of our original number that still hasn’t been converted to hexadecimal. Repeat this process on our remainder of by first checking if (which it is). Repeat our long division step yet again:

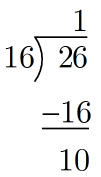
If you are starting to find this process repetitive, then you are getting the idea. This is an algorithm! Our next hexadecimal digit is the quotient from our most recent division step, . There’s only one last square to fill in: .

The remainder from the above division step is . Since it is clear that $16^0 \leq 10$, we just need to perform a final long division step:

Our last digit is when described in base 10, or in hexadecimal. Our number is , as expected. Note that the remainder of in our last division step indicates that it is time to terminate this process.

We should probably do another example, but with less wordiness. The main thing to notice is that this algorithm is just repeated long division. The quotient from each long division represents a hexadecimal digit, and the remainder is the number that we use when we repeat the process.

Converting to Octal (Base 8)

This time, we are going to convert the number from decimal (base 10) to octal (base 8). We first need to find the largest value of such that . Guess-and-check or computing quickly reveals that is the largest power of that is less than . We are expecting a digit number to describe in octal (base 8).

Use long division to determine the first digit of our octal number:

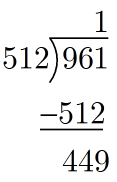
Our number (so far) is . Use the remainder of for our next division with a divisor of :

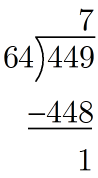
Now our number looks like . Use the remainder of for our next division with a divisor of :

Since , you can see why this division step has a quotient of 0. Now our octal (base 8) number looks like . Just one more digit to go! Use $1$ again for our next division with a divisor of :

Finally, we have .

Is There an Easier Way?

This technique relies heavily on long division. But if you want to write a computer program that converts a decimal number to base b, you might wonder if there’s an easy way to “do long division” in a computer. The answer is yes. Let’s repeat our conversion one more time. This time, we will try to use our knowledge of computers to make this process a bit easier. Instead of performing long division, you just need to find the quotient and remainder from this process. You can find a quotient of by asking the computer for the integer part of . For our pseudocode, we will let div represent the integer part of our division (also known as integer division). Similarly, you can find the remainder of the division by finding . For our pseudocode, we will write this as a % b.

1. first exponent of 8: k = integer part of log(961)/log(8) = 3
2. first digit: d3 = 961 div 8^3 = 1 and remainder: r3 = 961 % 8^3 = 449
3. second digit:d2 = 449 div 8^2 = 7 and remainder: r2 = 449 % 8^2 = 1
4. third digit: d1 = 1 div 8^1 = 0 and remainder: r1 = 1 % 8^1 = 1
5. fourth digit: d0 = 1 div 8^0 = 1 and remainder: r0 = 1 % 8^0 = 0
6. result: d3d2d1d0 = 1701

Converting to Binary (Base 2)

This process will work for any integer number base . So we should be able to use it to convert to binary (base 2). Let’s convert the decimal number to binary.

1. first exponent of 2: k = integer part of log(38)/log(2) = 5
2. first digit: d5 = 38 div 2^5 = 1 and remainder: r5 = 45 % 2^5 = 6
3. second digit:d4 = 6 div 2^4 = 0 and remainder: r4 = 6 % 2^4 = 6
4. third digit: d3 = 6 div 2^3 = 0 and remainder: r3 = 6 % 2^3 = 6
5. fourth digit: d2 = 6 div 2^2 = 1 and remainder: r2 = 6 % 2^2 = 2
6. fifth digit: d1 = 2 div 2^1 = 1 and remainder: r1 = 2 % 2^1 = 0
7. sixth digit: d0 = 0 div 2^0 = 0 and remainder: r0 = 0 % 2^0 = 0
8. result: d5d4d3d2d1d0 = 100110

Hence, we have that . If you are not a fan of this pseudocode calculation, you can still use long division to get the same result:

Again, we see that .

An Algorithm to Convert Decimal (base 10) to base b

Now that you have a pretty good idea of how to convert from base b to base 10, how would you write a computer program to complete this task for you? The steps that your program will need to follow is called an algorithm. In general, it is a good idea to

1. Write the steps of your algorithm in your own words (in plain English). Try your steps out on an example and see if you missed anything.
2. Write out the steps of your algorithm in pseudocode. Pay particular attention what your function takes as input, what it produces as output, and what steps need to happen in between to turn your input into your desired output. Again, try out your steps on an example and see if you missed anything.
3. Convert your pseudocode to actual code in your language of choice. Make sure to put comments in your code. You should also spend some time testing what you created. Does your algorithm produce the expected output for some simple calculations? Finally, test the limits of your code. Does your program handle user input that doesn’t make sense or somehow “breaks the rules”? For example, you should not be able to convert a number from base 1 since this number base doesn’t exist!

Practice Problems

Here are a few practice problems to try on your own:

Next Steps

Now that you are comfortable with converting from base 10 to base b and from base b to base 10, you may want to read my next post about how to easily convert between binary and hexadecimal. The title of this post is Bits, Bytes, and Binary.

Finally, if you want some more practice, you can make up your own problemas using this number base conversion tool.